class: title-slide, center, inverse # Meta-analyses in `R` # ## Matteo Lisi ### 2023/2/22 --- class: inverse # Outline 1. Effect sizes 2. Estimating meta-analytic models in R (`metafor` package, Viechtbauer (2010)) + Random-effects model + Meta-regression + Multilevel meta analysis 5. Bias detection --- name: eff_size # Effect sizes -- - A summary statistics that capture the _direction_ and _size_ of the "effect" of interest (e.g. the mean difference between two conditions, groups, etc.) -- - _Unstandardized_ vs. _standardized_ -- - Standardize effect size measures should be used when it is not possible to quantify express results in the same units across different studies; e.g. see Baguley (2009) -- - Example: standardized mean difference `\(\text{Cohen's }d = \frac{\text{mean difference}}{\text{expected variation of individual observation}}\)` - For two independent groups: `\(\text{Cohen's }d = \frac{{\overline{M}}_{1}{-\overline{M}}_{2}}{\text{SD}_{\text{pooled}}}\)` --- class: inverse ### Effect size reliability For each effect size we need to know how reliable it is. This is typically quantified by the _standard error of the effect size_. -- Formally we have: - `\(\theta_k\)` .orange[is the _'true'_ (but unknown) effect size] of study `\(k\)` - `\(\hat \theta_k = \theta_k + \epsilon_k\)` is the .orange[_observed_ effect size] - `\(\epsilon_k\)` is the .orange['sampling error'] -- The sampling error is the 'uncontrolled' variability (accounting for the fact that even an exact replication of a study would likely give a different result). -- If we were to repeat the experiment many times (ideally infinitely many) we would obtain the .orange[_sampling distribution_] of the observed effect `\(\hat \theta_k\)`. -- Given a single study, we can never know `\(\epsilon_k\)`, however we can estimate it's variability. The .orange[standard error (_SE_)] of the effect size is the standard deviation of the sampling distribution, and therefore it is an estimate of how reliable is a study. --- ### Effect size reliability Example: the standard error of the mean is `$$SE = \frac{s}{\sqrt{n}}$$` where `\(s\)` is the sample standard deviation and `\(n\)` the sample size. As `\(n\)` increases, the standard error will decrease proportionally to `\(\sqrt{n}\)`. -- e.g. study A has twice the sample size of study B -- `\(\implies\)` the sampling error of study A is expected to be `\(\frac{1}{\sqrt{2}} \approx 70\%\)` that of study B. --- ### Cohen's `\(d\)` reliability Standard error's for Cohen's `\(d\)`: `$$SE(d) = \sqrt{\frac{n_1+n_2}{n_1n_2} + \frac{d^2}{2(n_1+n_2)}}$$` --- ### Effect size: range considerations For the meta-analytic approach taken in `metafor`, we need to ensure that effect size measures are not restricted in their range -- - if the effect size is a proportion (range restricted between 0 and 1), we can transform this in log-odds: `$$\text{log-odds} = \log \left(\frac{p}{1-p}\right), \qquad SE_{\text{log-odds}}=\sqrt{\frac{1}{np}+\frac{1}{n(1-p)}}$$` -- - if the effect size is a correlation (range restricted between -1 and 1), we can use Fisher's `\(z\)` transform: `$$z = 0.5\log \left(\frac{1+r}{1-r}\right), \qquad SE_{z} = \frac{1}{\sqrt{n-3}}$$` --- ### Effect size: exercise The dataset `power_pose` contains 6 pre-registered replications testing whether participants reported higher "feeling-of-power" ratings after adopting expansive 'as opposed to constrictive body postures. ```r power_pose <- read.csv("https://mlisi.xyz/files/workshops/meta_analyses/data/power_pose.csv") str(power_pose) ``` ``` ## 'data.frame': 6 obs. of 7 variables: ## $ study : chr "Bailey et al." "Ronay et al." "Klaschinski et al." "Bombari et al." ... ## $ n_high_power : int 46 53 101 99 100 135 ## $ n_low_power : int 48 55 99 101 100 134 ## $ mean_high_power: num 2.62 2.12 3 2.24 2.58 ... ## $ mean_low_power : num 2.39 1.95 2.73 1.99 2.44 ... ## $ sd_high_power : num 0.932 0.765 0.823 0.927 0.789 ... ## $ sd_low_power : num 0.935 0.792 0.9 0.854 0.977 ... ``` -- `\(\\[0.3in]\)` .red[ 1. Calculate standardized effect size (Cohen's `\(d\)`) and its standard error for each study, and add it as an additional column in the dataset. 2. Additional: Compute also the `\(t\)` statistic and the one-sided p-value for each study ] --- .blue[Formulae:] .pull-left[ `$$\text{Cohen's }d = \frac{{\overline{M}}_{1}{-\overline{M}}_{2}}{\sigma_{\text{pooled}}}$$` `$$SE(d) = \sqrt{\frac{n_1+n_2}{n_1n_2} + \frac{d^2}{2(n_1+n_2)}}$$` `$$\sigma_{\text{pooled}} = \sqrt{ \frac{(n_1-1)\sigma^2_1 + (n2-1)\sigma^2_2}{n_1 + n_2 -2}}$$` ] -- .pull-right[ `$$t = \frac{{\overline{M}}_{1}{-\overline{M}}_{2}}{\sigma_{\text{pooled}}\sqrt{\frac{1}{n1} + \frac{1}{n2}}}$$` ] `\(\\[1in]\)` -- .red[ 1. Calculate standardized effect size (Cohen's `\(d\)`) and its standard error for each study, and add it as an additional column in the dataset. 2. Additional: Compute also the `\(t\)` statistic and the one-sided p-value for each study ] --- ```r # function for computing pooled SD pooled_SD <- function(sdA,sdB,nA,nB){ sqrt((sdA^2*(nA-1) + sdB^2*(nB-1))/(nA+nB-1)) } # function for Cohen's d cohen_d_se <- function(n1,n2,d){ sqrt((n1+n2)/(n1*n2) + (d^2)/(2*(n1+n2))) } # apply functions & create new columns in the dataset (using dplyr::mutate) power_pose <- power_pose %>% mutate(pooled_sd =pooled_SD(sd_high_power, sd_low_power, n_high_power, n_low_power), mean_diff = mean_high_power - mean_low_power, cohen_d = mean_diff/pooled_sd, SE = cohen_d_se(n_high_power, n_low_power,cohen_d)) ``` --- ```r # function for computing pooled SD pooled_SD <- function(sdA,sdB,nA,nB){ sqrt((sdA^2*(nA-1) + sdB^2*(nB-1))/(nA+nB-1)) } # function for Cohen's d cohen_d_se <- function(n1,n2,d){ sqrt((n1+n2)/(n1*n2) + (d^2)/(2*(n1+n2))) } # apply functions & create new columns in the dataset (base R) power_pose$pooled_sd <- with(power_pose, pooled_SD(sd_high_power, sd_low_power, n_high_power, n_low_power)) power_pose$mean_diff <- with(power_pose, mean_high_power - mean_low_power) power_pose$cohen_d <- with(power_pose, mean_diff/pooled_sd) power_pose$SE <- with(power_pose, cohen_d_se(n_high_power, n_low_power,cohen_d)) ``` --- ```r par(mfrow=c(1,2)) n <- with(power_pose, n_high_power + n_low_power) plot(n,power_pose$SE, ylab="SE(Cohen's d)",cex=1.5) plot(power_pose$mean_diff, power_pose$cohen_d, xlab = "mean difference (5-point Likert scale)", ylab="Cohen's d",cex=1.5) ``` <img src="meta_analyses_slides_files/figure-html/unnamed-chunk-5-1.svg" style="display: block; margin: auto;" /> --- name: meta_analyses # Meta-analyses: pooling effect sizes -- <img src="meta_analyses_slides_files/figure-html/unnamed-chunk-7-1.svg" style="display: block; margin: auto;" /> --- class:inverse ## Random-effects model We have defined `\(\theta_k\)` as the _true_ effect size of study `\(k\)` and `\(\hat \theta_k = \theta_k + \epsilon_k\)` as the _observed_ effect size. -- In the random-effects model, we further assume that `\(\theta_k\)` is a random sample from a population of possible studies that measure the same effect but differ in their methods or sample characteristics. These differences introduce .orange[heterogeneity] among the true effects. -- The random-effects model account for this heterogeneity by treating as an _additional level of randomness_; that is we assume that `$$\theta_k = \mu + \zeta_k$$` where `\(\mu\)` is the average of true effects, and `\(\zeta_k \sim \mathcal{N}(0, \tau^2)\)` are random, study-specific fluctuations in the true effect. The variance `\(\tau^2\)` quantifies the amount of heterogeneity among true effects. -- --- class:inverse ## Random-effects model Putting it all together we have that `$$\hat \theta_k = \mu + \zeta_k + \epsilon_k$$` with `$$\zeta_k \sim \mathcal{N}(0, \tau^2) \\ \epsilon_k \sim \mathcal{N}(0, \sigma^2_k)$$` `\(\\[1in]\)` -- Or equivalently, in more compact notation: `$$\hat \theta_k \sim \mathcal{N}(\theta_k, \sigma^2_k), \quad \theta_k\sim \mathcal{N}(\mu, \tau^2)$$` --- ## `metafor` package The function `rma` allows to fit the random-effects model very easily. -- For the `power_pose` example ```r str(power_pose) ``` ``` ## 'data.frame': 6 obs. of 11 variables: ## $ study : chr "Bailey et al." "Ronay et al." "Klaschinski et al." "Bombari et al." ... ## $ n_high_power : int 46 53 101 99 100 135 ## $ n_low_power : int 48 55 99 101 100 134 ## $ mean_high_power: num 2.62 2.12 3 2.24 2.58 ... ## $ mean_low_power : num 2.39 1.95 2.73 1.99 2.44 ... ## $ sd_high_power : num 0.932 0.765 0.823 0.927 0.789 ... ## $ sd_low_power : num 0.935 0.792 0.9 0.854 0.977 ... ## $ pooled_sd : num 0.929 0.775 0.86 0.889 0.886 ... ## $ mean_diff : num 0.234 0.177 0.275 0.252 0.13 ... ## $ cohen_d : num 0.252 0.229 0.319 0.284 0.147 ... ## $ SE : num 0.207 0.193 0.142 0.142 0.142 ... ``` we can estimate the model with this command: ```r library(metafor) res <- rma(cohen_d, SE^2, data = power_pose) ``` --- Model output: ```r summary(res) ``` ``` ## ## Random-Effects Model (k = 6; tau^2 estimator: REML) ## ## logLik deviance AIC BIC AICc ## 4.0374 -8.0748 -4.0748 -4.8559 1.9252 ## ## tau^2 (estimated amount of total heterogeneity): 0 (SE = 0.0139) ## tau (square root of estimated tau^2 value): 0 ## I^2 (total heterogeneity / total variability): 0.00% ## H^2 (total variability / sampling variability): 1.00 ## ## Test for Heterogeneity: ## Q(df = 5) = 1.2981, p-val = 0.9351 ## ## Model Results: ## ## estimate se zval pval ci.lb ci.ub ## 0.2230 0.0613 3.6358 0.0003 0.1028 0.3432 *** ## ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- ## Measures of heterogeneity In the random-effects model the `\(\tau^2\)` directly quantify the heterogeneity. -- There are other measures of of heterogeneity which can be applied also to non random-effects models: - Cochran’s `\(Q\)` statistic - `\(I^2\)` statistic - `\(H^2\)` statistic --- ### Cochran’s `\(Q\)` statistic Weighted sum of the squared differences between effect size estimates in each study, `\(\hat \theta_k\)`, and the meta-analytic effect size estimate, `\(\hat \mu_k\)` `$$Q = \sum^K_{k=1}w_k(\hat\theta_k-\hat\mu)^2$$` where `\(w_k = \frac{1}{\sigma^2_k}\)` -- Under the null hypothesis that all effect size differences are caused only by sampling error (no heterogeneity), `\(Q\)` is approximately distributed as `\(\chi^2\)` with `\(K-1\)` degrees of freedom. --- ### `\(I^2\)` statistic Percentage of variability in the observed effect sizes that is not caused by sampling error $$ I^2 = \frac{Q-(K-1)}{Q}%$$ where `\(K\)` is the total number of studies. --- ### `\(H^2\)` statistic `$$H^2 = \frac{Q}{K-1}$$` It can be interpreted as the ratio of the observed variation, and the expected variance due to sampling error. `\(H^2>1\)` indicates heterogeneity --- Model output: ```r summary(res) ``` ``` ## ## Random-Effects Model (k = 6; tau^2 estimator: REML) ## ## logLik deviance AIC BIC AICc ## 4.0374 -8.0748 -4.0748 -4.8559 1.9252 ## ## tau^2 (estimated amount of total heterogeneity): 0 (SE = 0.0139) ## tau (square root of estimated tau^2 value): 0 ## I^2 (total heterogeneity / total variability): 0.00% ## H^2 (total variability / sampling variability): 1.00 ## ## Test for Heterogeneity: ## Q(df = 5) = 1.2981, p-val = 0.9351 ## ## Model Results: ## ## estimate se zval pval ci.lb ci.ub ## 0.2230 0.0613 3.6358 0.0003 0.1028 0.3432 *** ## ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- Since `\(\tau^2 \approx 0\)`, we could also estimate a fixed-effect model (option `method="FE"`) ```r summary(rma(cohen_d, SE^2, data = power_pose, method="FE")) ``` ``` ## ## Fixed-Effects Model (k = 6) ## ## logLik deviance AIC BIC AICc ## 5.0141 1.2981 -8.0283 -8.2365 -7.0283 ## ## I^2 (total heterogeneity / total variability): 0.00% ## H^2 (total variability / sampling variability): 0.26 ## ## Test for Heterogeneity: ## Q(df = 5) = 1.2981, p-val = 0.9351 ## ## Model Results: ## ## estimate se zval pval ci.lb ci.ub ## 0.2230 0.0613 3.6358 0.0003 0.1028 0.3432 *** ## ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- The `metafor` package has also a handy function to make .purple[forest plots]: ```r forest(res) ``` <img src="meta_analyses_slides_files/figure-html/unnamed-chunk-13-1.svg" style="display: block; margin: auto;" /> --- With only a few addition we can make a publication-quality figure ```r forest(res, slab=study, xlim=c(-5,2), xlab="Cohen's d", ilab=round(cbind(with(power_pose, n_high_power + n_low_power), mean_low_power, sd_low_power, mean_high_power, sd_high_power),digits=2), ilab.xpos=c(-3.5, -2.5,-2,-1.25,-0.75), cex=.75, header="Authors", mlab="") par(cex=.75, font=2) text(c(-2.5,-2,-1.25,-0.75), res$k+2, c("mean", "Std.", "mean", "Std.")) text(c(-2.25,-1), res$k+3, c("Low power", "High power")) text(-3.5, res$k+2, "N") # this add the results of the heterogeneity test text(-5, -1, pos=4, cex=0.9, bquote(paste("RE Model (Q = ",.(formatC(res$QE, digits=2, format="f")), ", df = ", .(res$k - res$p),", p = ", .(formatC(res$QEp, digits=2, format="f")), "; ", I^2, " = ", .(formatC(res$I2, digits=1, format="f")), "%)"))) ``` <img src="meta_analyses_slides_files/figure-html/unnamed-chunk-14-1.svg" style="display: block; margin: auto;" /> --- ## Random-effects model exercise 1. `towels` contains results of a set of studies that investigated whether people reuse towels in hotels more often if they are provided with a descriptive norm (a message stating that the majority of guests actually reused their towels), as opposed to a control condition in which they were simply encouraged to reuse the towels (with a message about the protection of the environment) ```r towels <- read.csv("https://mlisi.xyz/files/workshops/meta_analyses/data/towels.csv") str(towels) ``` ``` ## 'data.frame': 7 obs. of 3 variables: ## $ study: chr "Goldstein, Cialdini, & Griskevicius (2008), Exp. 1" "Goldstein, Cialdini, & Griskevicius (2008), Exp. 2" "Schultz, Khazian, & Zaleski (2008), Exp. 2" "Schultz, Khazian, & Zaleski (2008), Exp. 3" ... ## $ logOR: num 0.381 0.305 0.206 0.251 0.288 ... ## $ SE : num 0.198 0.136 0.192 0.17 0.824 ... ``` --- ## Random-effects model exercise 2. `ThirdWave` studies examining the effect of so-called “third wave” psychotherapies on perceived stress in college students. The effect size is the standardized mean difference between a treatment and control group at post-test ```r load(url('https://mlisi.xyz/files/workshops/meta_analyses/data/thirdwave.rda')) str(ThirdWave) ``` ``` ## 'data.frame': 18 obs. of 8 variables: ## $ Author : chr "Call et al." "Cavanagh et al." "DanitzOrsillo" "de Vibe et al." ... ## $ TE : num 0.709 0.355 1.791 0.182 0.422 ... ## $ seTE : num 0.261 0.196 0.346 0.118 0.145 ... ## $ RiskOfBias : chr "high" "low" "high" "low" ... ## $ TypeControlGroup : chr "WLC" "WLC" "WLC" "no intervention" ... ## $ InterventionDuration: chr "short" "short" "short" "short" ... ## $ InterventionType : chr "mindfulness" "mindfulness" "ACT" "mindfulness" ... ## $ ModeOfDelivery : chr "group" "online" "group" "group" ... ``` Example taken from the [book](https://bookdown.org/MathiasHarrer/Doing_Meta_Analysis_in_R/) by Harrer, Cuijpers, A, and Ebert (2021). --- # Meta-analytic regression Study-level variables ('moderators') can also be included as predictors in meta-analytic models, leading to so-called 'meta-regression' analyses. Example, with 1 study-level moderator variable `\(X_k\)` `$$\hat \theta_k = \beta_0 + \beta X_k + \zeta_k + \epsilon_k$$` where the intercept `\(\beta_0\)` corresponds to the average true effect/outcome `\(\mu\)` when the value of the moderator variable `\(X_k\)` is equal to zero. --- ### Meta-analytic regression example <div id="htmlwidget-9ecb91dc44a8efad0273" style="width:100%;height:auto;" class="datatables html-widget"></div> <script type="application/json" data-for="htmlwidget-9ecb91dc44a8efad0273">{"x":{"filter":"none","vertical":false,"fillContainer":false,"data":[["1","2","3","4","5","6","7","8","9","10","11","12","13","14","15","16","17","18"],["Call et al.","Cavanagh et al.","DanitzOrsillo","de Vibe et al.","Frazier et al.","Frogeli et al.","Gallego et al.","Hazlett-Stevens & Oren","Hintz et al.","Kang et al.","Kuhlmann et al.","Lever Taylor et al.","Phang et al.","Rasanen et al.","Ratanasiripong","Shapiro et al.","Song & Lindquist","Warnecke et al."],[0.709136234756933,0.354864109077645,1.79117003272488,0.182455216323761,0.42185093084487,0.63,0.724883808783712,0.528663812357321,0.284,1.27506817139631,0.10360817637506,0.388390560376566,0.540739823331358,0.426159311552595,0.515396915332498,1.47972601084922,0.612578239930467,0.6],[0.260820178547769,0.196362410818884,0.345569205699001,0.117787401662918,0.144812762024237,0.196,0.224664137749212,0.210460918848162,0.168,0.337199688565405,0.194727463484504,0.230768893346391,0.244313267301974,0.257937944593587,0.351273746997289,0.315281680355345,0.226683364977455,0.249],["high","low","high","low","low","low","high","low","low","low","high","low","low","low","high","high","high","low"],["WLC","WLC","WLC","no intervention","information only","no intervention","no intervention","no intervention","information only","no intervention","no intervention","WLC","no intervention","WLC","no intervention","WLC","WLC","information only"],["short","short","short","short","short","short","long","long","short","long","short","long","short","short","short","long","long","long"],["mindfulness","mindfulness","ACT","mindfulness","PCI","ACT","mindfulness","mindfulness","PCI","mindfulness","mindfulness","mindfulness","mindfulness","ACT","mindfulness","mindfulness","mindfulness","mindfulness"],["group","online","group","group","online","group","group","book","online","group","group","book","group","online","group","group","group","online"]],"container":"<table class=\"display\">\n <thead>\n <tr>\n <th> <\/th>\n <th>Author<\/th>\n <th>TE<\/th>\n <th>seTE<\/th>\n <th>RiskOfBias<\/th>\n <th>TypeControlGroup<\/th>\n <th>InterventionDuration<\/th>\n <th>InterventionType<\/th>\n <th>ModeOfDelivery<\/th>\n <\/tr>\n <\/thead>\n<\/table>","options":{"pageLength":12,"initComplete":"function(settings, json) {\n$(this.api().table().container()).css({'font-size': '7pt'});\n}","columnDefs":[{"targets":2,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"targets":3,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"className":"dt-right","targets":[2,3]},{"orderable":false,"targets":0}],"order":[],"autoWidth":false,"orderClasses":false,"lengthMenu":[10,12,25,50,100]}},"evals":["options.initComplete","options.columnDefs.0.render","options.columnDefs.1.render"],"jsHooks":[]}</script> --- Does the duration of intervention influence the effect size? ```r # transform duration in a dummy variable ThirdWave$duration_dummy <- ifelse(ThirdWave$InterventionDuration=="long", 1, 0) res2 <- rma(yi=TE, vi=seTE^2, data = ThirdWave, mods = duration_dummy) print(res2) ``` ``` ## ## Mixed-Effects Model (k = 18; tau^2 estimator: REML) ## ## tau^2 (estimated amount of residual heterogeneity): 0.0630 (SE = 0.0401) ## tau (square root of estimated tau^2 value): 0.2510 ## I^2 (residual heterogeneity / unaccounted variability): 58.30% ## H^2 (unaccounted variability / sampling variability): 2.40 ## R^2 (amount of heterogeneity accounted for): 23.13% ## ## Test for Residual Heterogeneity: ## QE(df = 16) = 37.5389, p-val = 0.0018 ## ## Test of Moderators (coefficient 2): ## QM(df = 1) = 2.6694, p-val = 0.1023 ## ## Model Results: ## ## estimate se zval pval ci.lb ci.ub ## intrcpt 0.4701 0.1001 4.6970 <.0001 0.2739 0.6663 *** ## mods 0.2739 0.1676 1.6338 0.1023 -0.0547 0.6025 ## ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- .red[Does adding the moderators significantly improve the ability of the model to explain the observed effect sizes?] ```r # refit models using maximum likelihood estimation (ML) res0 <- rma(yi=TE, vi=seTE^2, data = ThirdWave, method="ML") res2 <- rma(yi=TE, vi=seTE^2, data = ThirdWave, mods = duration_dummy, method="ML") # run likelihood ratio test of nested models anova(res0, res2) ``` ``` ## ## df AIC BIC AICc logLik LRT pval QE tau^2 ## Full 3 20.6903 23.3614 22.4046 -7.3452 37.5389 0.0423 ## Reduced 2 21.5338 23.3145 22.3338 -8.7669 2.8435 0.0917 45.5026 0.0715 ## R^2 ## Full ## Reduced 40.7999% ``` --- # "Multi-level" meta analysis `\(\quad \quad\)` (AKA three-level meta analysis) -- Introduce a hierarchically higher level of randomness in which observed effect sizes are grouped in "clusters" that share some similarities (for example many effect sizes are nested in one study; or many studies are nested in subgroups depending on the nationality of the participants). -- Formally `$$\hat\theta_{ij} = \mu + \zeta_{(2)ij} + \zeta_{(3)j} + \epsilon_{ij}$$` --- ### Three-level meta analysis example ```r load(url('https://mlisi.xyz/files/workshops/meta_analyses/data/Chernobyl.rda')) str(Chernobyl) ``` ``` ## 'data.frame': 33 obs. of 8 variables: ## $ author : chr "Aghajanyan & Suskov (2009)" "Aghajanyan & Suskov (2009)" "Aghajanyan & Suskov (2009)" "Aghajanyan & Suskov (2009)" ... ## $ cor : num 0.206 0.269 0.205 0.267 0.932 ... ## $ n : num 91 91 92 92 559 559 559 559 559 559 ... ## $ z : num 0.209 0.275 0.208 0.274 1.671 ... ## $ se.z : num 0.1066 0.1066 0.106 0.106 0.0424 ... ## $ var.z : num 0.0114 0.0114 0.0112 0.0112 0.0018 ... ## $ radiation: chr "low" "low" "low" "low" ... ## $ es.id : chr "id_1" "id_2" "id_3" "id_4" ... ``` --- ### Three-level meta analysis example <div id="htmlwidget-3577faeaba68550340af" style="width:100%;height:auto;" class="datatables html-widget"></div> <script type="application/json" data-for="htmlwidget-3577faeaba68550340af">{"x":{"filter":"none","vertical":false,"fillContainer":false,"data":[["1","2","3","4","5","6","7","8","9","10","11","12","13","14","15","16","17","18","19","20","21","22","23","24","25","26","27","28","29","30","31","32","33"],["Aghajanyan & Suskov (2009)","Aghajanyan & Suskov (2009)","Aghajanyan & Suskov (2009)","Aghajanyan & Suskov (2009)","Alexanin et al. (2010)","Alexanin et al. (2010)","Alexanin et al. (2010)","Alexanin et al. (2010)","Alexanin et al. (2010)","Alexanin et al. (2010)","Bochkov (1993)","Bochkov (1993)","Dubrova et al. (1996)","Dubrova et al. (1997)","Dubrova et al. (1998)","Dubrova et al. (1998)","Dubrova et al. (2002)","Dubrova et al. (2002)","Dubrova et al. (2002)","Forster et al. (2002)","Khandogina (2010)","Kodaira et al. (2010)","Kodaira et al. (2010)","Kodaira et al. (2010)","Maznik & Vinnikov (2004)","Neronova et al. (2003)","Neronova et al. (2003)","Neronova et al. (2003)","Stepanova & Misharina (2001)","Stepanova & Misharina (2001)","Stepanova & Misharina (2001)","Stepanova & Misharina (2001)","Weinberg et al. (2001)"],[0.2061,0.2687,0.2049,0.2672,0.9317,0.4429,0.8996,0.9547,0.9602,0.6335,0.2732,0.833,0.2975,0.418,0.3596,0.4015,0.1177,-0.1932,0.1409,0.0767,0.7594,0.0155,-0.0539,0.0461,0.4289,0.0783,0.147,0.14,0.7478,0.8834,0.8725,0.7319,0.8008],[91,91,92,92,559,559,559,559,559,559,560,15,79,94,127,127,256,256,256,988,69,129,129,129,470,442,442,442,57,57,57,57,63],[0.209094891929065,0.275462130434823,0.207841981010897,0.27384610385012,1.67112297831775,0.47583274963822,1.47011820470867,1.88234248773499,1.94846743777234,0.747240854857209,0.280318679442961,1.19785771771147,0.306774606916071,0.445266129680317,0.376426418349701,0.425435922803408,0.118248073581753,-0.195659123280268,0.141843686979156,0.0768509390215445,0.994796158638998,0.0155012414706296,-0.0539522881147463,0.0461326990992764,0.458547935402054,0.0784606074442041,0.148072784818846,0.140925576070494,0.967945354831312,1.39104232957979,1.34345667539645,0.932807152746542,1.10083847222101],[0.106600358177805,0.106600358177805,0.105999788000636,0.105999788000636,0.0424094464839985,0.0424094464839985,0.0424094464839985,0.0424094464839985,0.0424094464839985,0.0424094464839985,0.0423713598607036,0.288675134594813,0.114707866935281,0.104828483672192,0.0898026510133875,0.0898026510133875,0.0628694613461931,0.0628694613461931,0.0628694613461931,0.0318626493938583,0.123091490979333,0.0890870806374748,0.0890870806374748,0.0890870806374748,0.0462744813382748,0.0477273959903348,0.0477273959903348,0.0477273959903348,0.136082763487954,0.136082763487954,0.136082763487954,0.136082763487954,0.129099444873581],[0.0113636363636364,0.0113636363636364,0.0112359550561798,0.0112359550561798,0.00179856115107914,0.00179856115107914,0.00179856115107914,0.00179856115107914,0.00179856115107914,0.00179856115107914,0.00179533213644524,0.0833333333333333,0.0131578947368421,0.010989010989011,0.00806451612903226,0.00806451612903226,0.00395256916996047,0.00395256916996047,0.00395256916996047,0.00101522842639594,0.0151515151515152,0.00793650793650794,0.00793650793650794,0.00793650793650794,0.00214132762312634,0.00227790432801822,0.00227790432801822,0.00227790432801822,0.0185185185185185,0.0185185185185185,0.0185185185185185,0.0185185185185185,0.0166666666666667],["low","low","low","low","low","low","low","low","low","low","medium","medium","low","low","low","low","low","low","low","low","medium","high","high","high",null,"low","low","low","high","high","high","high",null],["id_1","id_2","id_3","id_4","id_5","id_6","id_7","id_8","id_9","id_10","id_11","id_12","id_13","id_14","id_15","id_16","id_17","id_18","id_19","id_20","id_21","id_22","id_23","id_24","id_25","id_26","id_27","id_28","id_29","id_30","id_31","id_32","id_33"]],"container":"<table class=\"display\">\n <thead>\n <tr>\n <th> <\/th>\n <th>author<\/th>\n <th>cor<\/th>\n <th>n<\/th>\n <th>z<\/th>\n <th>se.z<\/th>\n <th>var.z<\/th>\n <th>radiation<\/th>\n <th>es.id<\/th>\n <\/tr>\n <\/thead>\n<\/table>","options":{"pageLength":8,"initComplete":"function(settings, json) {\n$(this.api().table().container()).css({'font-size': '7pt'});\n}","columnDefs":[{"targets":5,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"targets":6,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"targets":2,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"targets":4,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"className":"dt-right","targets":[2,3,4,5,6]},{"orderable":false,"targets":0}],"order":[],"autoWidth":false,"orderClasses":false,"lengthMenu":[8,10,25,50,100]}},"evals":["options.initComplete","options.columnDefs.0.render","options.columnDefs.1.render","options.columnDefs.2.render","options.columnDefs.3.render"],"jsHooks":[]}</script> -- Studies reported correlation between radioactivity die to the nuclear fallout and mutation rates in humans, caused by the 1986 Chernobyl reactor disaster. Most studies reported multiple effect sizes (e.g. because they used several methods to measure mutations or considered several subgroups, such as exposed parents versus their offspring). --- In R, we can fit a model using the `rma.mv` function and setting the `random` argument to indicate the clustering structure ```r model_cherobyl <- rma.mv(yi = z, V = var.z, slab = author, data = Chernobyl, random = ~ 1 | author/es.id, # equivalent formulations below: # random = list(~ 1 | author, ~ 1 | interaction(author,es.id)), # random = list(~ 1 | author, ~ 1 | es.id), method = "REML") summary(model_cherobyl) ``` ``` ## ## Multivariate Meta-Analysis Model (k = 33; method: REML) ## ## logLik Deviance AIC BIC AICc ## -21.1229 42.2458 48.2458 52.6430 49.1029 ## ## Variance Components: ## ## estim sqrt nlvls fixed factor ## sigma^2.1 0.1788 0.4229 14 no author ## sigma^2.2 0.1194 0.3455 33 no author/es.id ## ## Test for Heterogeneity: ## Q(df = 32) = 4195.8268, p-val < .0001 ## ## Model Results: ## ## estimate se zval pval ci.lb ci.ub ## 0.5231 0.1341 3.9008 <.0001 0.2603 0.7860 *** ## ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` --- ```r forest(model_cherobyl) ``` <img src="meta_analyses_slides_files/figure-html/unnamed-chunk-23-1.svg" style="display: block; margin: auto;" /> --- ### "Multi-level" meta analysis exercise: ```r library(metafor) dat <- dat.konstantopoulos2011 head(dat) ``` ``` ## ## district school study year yi vi ## 1 11 1 1 1976 -0.180 0.118 ## 2 11 2 2 1976 -0.220 0.118 ## 3 11 3 3 1976 0.230 0.144 ## 4 11 4 4 1976 -0.300 0.144 ## 5 12 1 5 1989 0.130 0.014 ## 6 12 2 6 1989 -0.260 0.014 ``` Results from 56 studies on the effects of modified school calendars (comparing more frequent but shorter intermittent breaks, to a longer summer break) on student achievement. The effect `yi` is the standardized difference between the groups in each study, and `vi` is the study variance. (More info about this dataset at this [link](https://wviechtb.github.io/metadat/reference/dat.konstantopoulos2011.html)) --- ### "Multi-level" meta analysis exercise <div id="htmlwidget-34d6b2b3dc48239b14cc" style="width:100%;height:auto;" class="datatables html-widget"></div> <script type="application/json" data-for="htmlwidget-34d6b2b3dc48239b14cc">{"x":{"filter":"none","vertical":false,"fillContainer":false,"data":[["1","2","3","4","5","6","7","8","9","10","11","12","13","14","15","16","17","18","19","20","21","22","23","24","25","26","27","28","29","30","31","32","33","34","35","36","37","38","39","40","41","42","43","44","45","46","47","48","49","50","51","52","53","54","55","56"],[11,11,11,11,12,12,12,12,18,18,18,27,27,27,27,56,56,56,56,58,58,58,58,58,58,58,58,58,58,58,71,71,71,86,86,86,86,86,86,86,86,91,91,91,91,91,91,108,108,108,108,108,644,644,644,644],[1,2,3,4,1,2,3,4,1,2,3,1,2,3,4,1,2,3,4,1,2,3,4,5,6,7,8,9,10,11,1,2,3,1,2,3,4,5,6,7,8,1,2,3,4,5,6,1,2,3,4,5,1,2,3,4],[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56],[1976,1976,1976,1976,1989,1989,1989,1989,1994,1994,1994,1976,1976,1976,1976,1997,1997,1997,1997,1976,1976,1976,1976,1976,1976,1976,1976,1976,1976,1976,1997,1997,1997,1997,1997,1997,1997,1997,1997,1997,1997,2000,2000,2000,2000,2000,2000,2000,2000,2000,2000,2000,1995,1995,1994,1994],[-0.18,-0.22,0.23,-0.3,0.13,-0.26,0.19,0.32,0.45,0.38,0.29,0.16,0.65,0.36,0.6,0.08,0.04,0.19,-0.06,-0.18,0,0,-0.28,-0.04,-0.3,0.07,0,0.05,-0.08,-0.09,0.3,0.98,1.19,-0.07,-0.05,-0.01,0.02,-0.03,0,0.01,-0.1,0.5,0.66,0.2,0,0.05,0.07,-0.52,0.7,-0.03,0.27,-0.34,0.12,0.61,0.04,-0.05],[0.118,0.118,0.144,0.144,0.014,0.014,0.015,0.024,0.023,0.043,0.012,0.02,0.004,0.004,0.007,0.019,0.007,0.005,0.004,0.02,0.018,0.019,0.022,0.02,0.021,0.006,0.007,0.007,0.007,0.007,0.015,0.011,0.01,0.001,0.001,0.001,0.001,0.001,0.001,0.001,0.001,0.01,0.011,0.01,0.009,0.013,0.013,0.031,0.031,0.03,0.03,0.03,0.087,0.082,0.067,0.067]],"container":"<table class=\"display\">\n <thead>\n <tr>\n <th> <\/th>\n <th>district<\/th>\n <th>school<\/th>\n <th>study<\/th>\n <th>year<\/th>\n <th>yi<\/th>\n <th>vi<\/th>\n <\/tr>\n <\/thead>\n<\/table>","options":{"pageLength":16,"initComplete":"function(settings, json) {\n$(this.api().table().container()).css({'font-size': '8pt'});\n}","columnDefs":[{"targets":5,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"targets":6,"render":"function(data, type, row, meta) {\n return type !== 'display' ? data : DTWidget.formatRound(data, 2, 3, \",\", \".\", null);\n }"},{"className":"dt-right","targets":[1,2,3,4,5,6]},{"orderable":false,"targets":0}],"order":[],"autoWidth":false,"orderClasses":false,"lengthMenu":[10,16,25,50,100]}},"evals":["options.initComplete","options.columnDefs.0.render","options.columnDefs.1.render"],"jsHooks":[]}</script> --- class:inverse # Bias detection Funnel plot .center[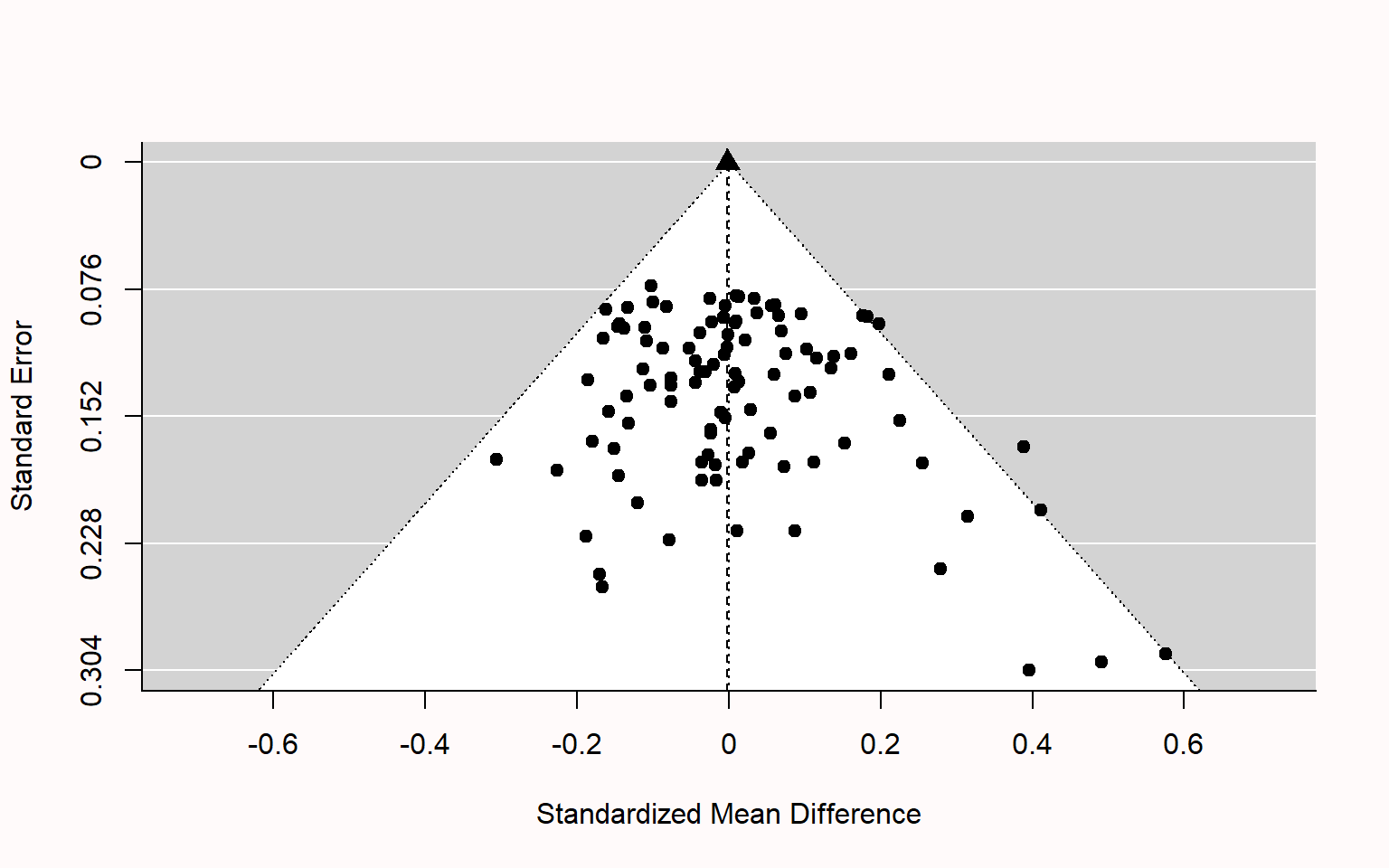] Image from Lakens (2023), [link](https://lakens.github.io/statistical_inferences/bias.html) --- class:inverse # Bias detection Funnel plot .center[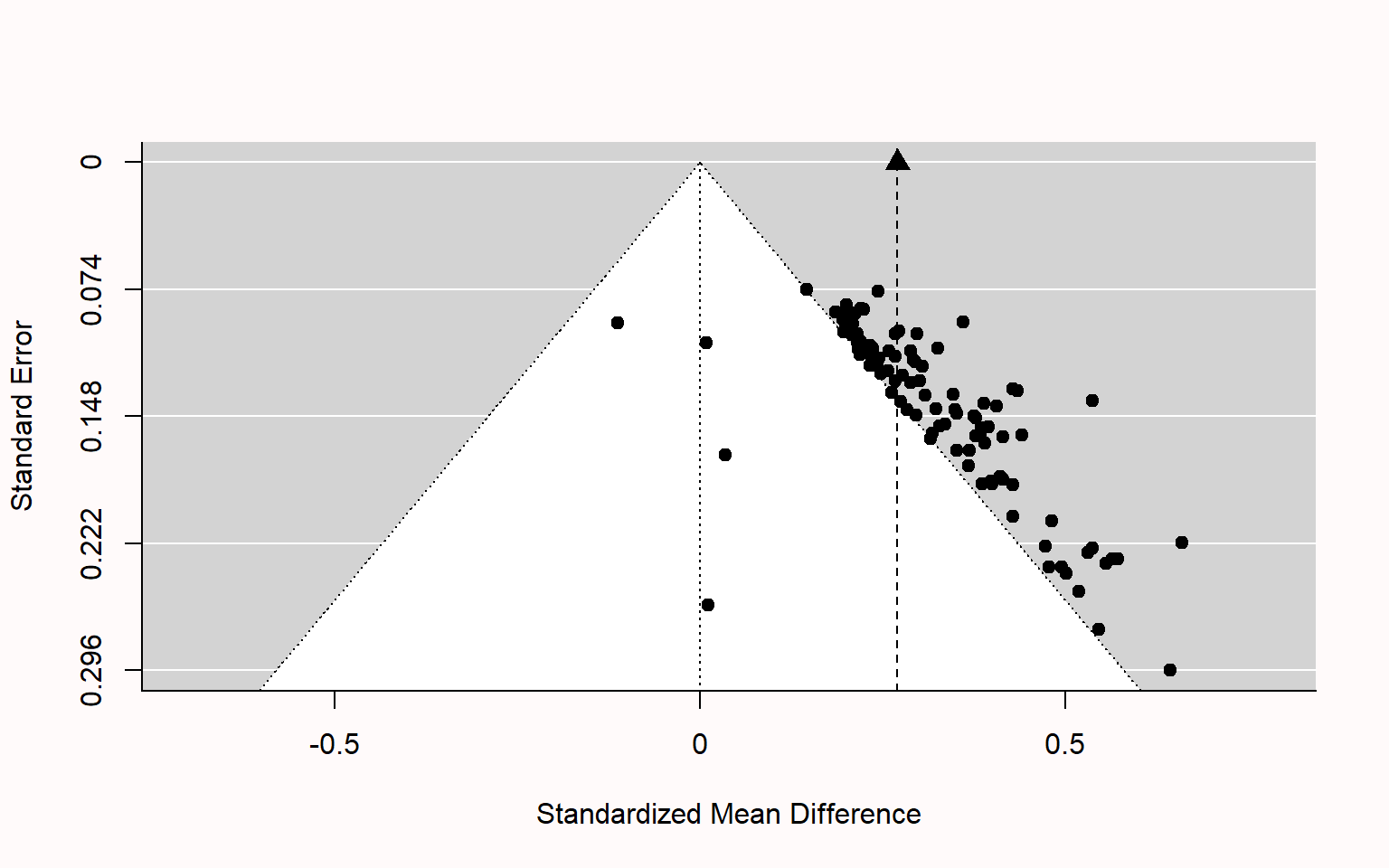] Image from Lakens (2023), [link](https://lakens.github.io/statistical_inferences/bias.html) --- class:inverse # Bias detection Funnel plot .center[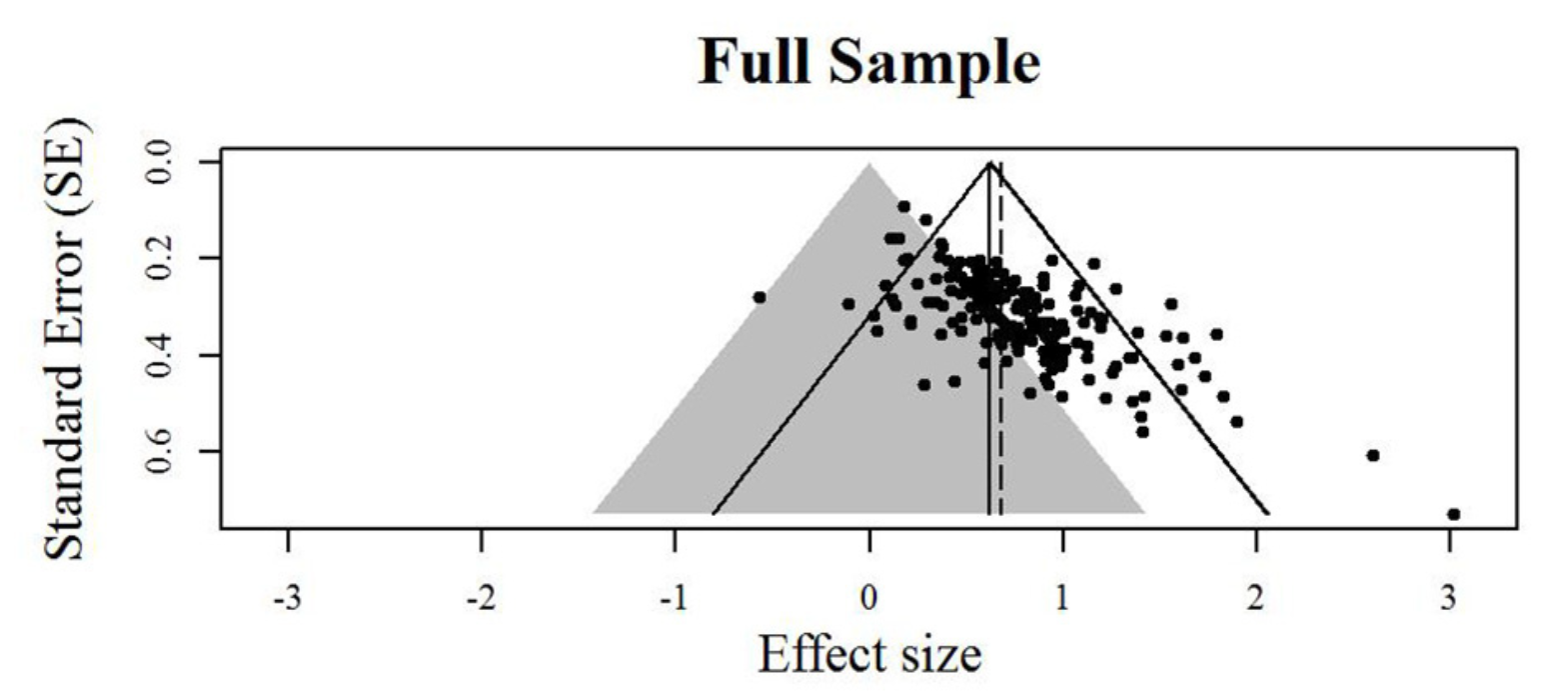] Funnel plot from Carter and McCullough (2014) vizualizing bias in 198 published tests of the ego-depletion effect. Image taken from Lakens (2023), [link](https://lakens.github.io/statistical_inferences/bias.html) --- #### Funnel plot for `ThirdWave` dataset ```r res <- rma(yi=TE, vi=seTE^2, data = ThirdWave) funnel(res, level=c(90, 95, 99), shade=c("white", "gray55", "gray75"), refline=0, legend=TRUE, xlab="Effect size (standardized mean difference)", refline2=res$b) ``` <img src="meta_analyses_slides_files/figure-html/unnamed-chunk-26-1.svg" style="display: block; margin: auto;" /> --- .orange[Egger’s regression test] for funnel plot asymmetry ```r regtest(res, model="lm") ``` ``` ## ## Regression Test for Funnel Plot Asymmetry ## ## Model: weighted regression with multiplicative dispersion ## Predictor: standard error ## ## Test for Funnel Plot Asymmetry: t = 4.6770, df = 16, p = 0.0003 ## Limit Estimate (as sei -> 0): b = -0.3407 (CI: -0.7302, 0.0487) ``` -- ```r with(ThirdWave, summary(lm(I(TE/seTE) ~ I(1/seTE)))) ``` ``` ## ## Call: ## lm(formula = I(TE/seTE) ~ I(1/seTE)) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.82920 -0.55227 -0.03299 0.66857 2.05815 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 4.1111 0.8790 4.677 0.000252 *** ## I(1/seTE) -0.3407 0.1837 -1.855 0.082140 . ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.096 on 16 degrees of freedom ## Multiple R-squared: 0.177, Adjusted R-squared: 0.1255 ## F-statistic: 3.44 on 1 and 16 DF, p-value: 0.08214 ``` --- Egger’s regression test `tidyverse` style ```r ThirdWave %>% mutate(y = TE/seTE, x = 1/seTE) %>% lm(y ~ x, data = .) %>% summary() ``` ``` ## ## Call: ## lm(formula = y ~ x, data = .) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.82920 -0.55227 -0.03299 0.66857 2.05815 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 4.1111 0.8790 4.677 0.000252 *** ## x -0.3407 0.1837 -1.855 0.082140 . ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.096 on 16 degrees of freedom ## Multiple R-squared: 0.177, Adjusted R-squared: 0.1255 ## F-statistic: 3.44 on 1 and 16 DF, p-value: 0.08214 ``` --- # References Baguley, T. (2009). "Standardized or simple effect size: What should be reported?" In: _British Journal of Psychology_ 100.3, pp. 603-617. DOI: https://doi.org/10.1348/000712608X377117. Harrer, M., P. Cuijpers, F. T. A, et al. (2021). _Doing Meta-Analysis With R: A Hands-On Guide_. 1st. Boca Raton, FL and London: Chapman & Hall/CRC Press. ISBN: 9780367610074. Lakens, D. (2023). _Improving Your Statistical Inferences_. <https://doi.org/10.5281/zenodo.6409077>. Viechtbauer, W. (2010). "Conducting meta-analyses in R with the metafor package". In: _Journal of Statistical Software_ 36.3, pp. 1-48. <https://doi.org/10.18637/jss.v036.i03>. --- ### Standardized effect size in LMMs -- Example: model on 2nd year marks of psychology students <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; text-align:left; ">&nbsp;</th> <th colspan="4" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">mark</th> </tr> <tr> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; text-align:left; ">Predictors</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">std. Error</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">CI</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">p</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">(Intercept)</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.6388</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.0235</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.5927&nbsp;&ndash;&nbsp;0.6850</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong>&lt;0.001</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">gender [male]</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">&#45;0.0317</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.0210</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">&#45;0.0730&nbsp;&ndash;&nbsp;0.0096</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.132</td> </tr> <tr> <td colspan="5" style="font-weight:bold; text-align:left; padding-top:.8em;">Random Effects</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">&sigma;²</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="4">0.0052</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">&tau;₀₀ _student</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="4">0.0095</td> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">&tau;₀₀ _module</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="4">0.0019</td> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">ICC</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="4">0.6851</td> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">N _student</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="4">163</td> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">N _module</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="4">4</td> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm; border-top:1px solid;">Observations</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="4">650</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">Marginal R² / Conditional R²</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="4">0.009 / 0.688</td> </tr> </table> --- ### Standardized effect size in LMMs Example: model on 2nd year marks of psychology students ``` ## Linear mixed model fit by REML ['lmerMod'] ## Formula: mark ~ gender + (1 | student) + (1 | module) ## Data: . ## ## REML criterion at convergence: -1201.4 ## ## Scaled residuals: ## Min 1Q Median 3Q Max ## -2.59763 -0.62613 0.03198 0.61472 2.32079 ## ## Random effects: ## Groups Name Variance Std.Dev. ## student (Intercept) 0.009515 0.09754 ## module (Intercept) 0.001882 0.04338 ## Residual 0.005238 0.07237 ## Number of obs: 650, groups: student, 163; module, 4 ## ## Fixed effects: ## Estimate Std. Error t value ## (Intercept) 0.63882 0.02349 27.190 ## gendermale -0.03174 0.02103 -1.509 ## ## Correlation of Fixed Effects: ## (Intr) ## gendermale -0.165 ``` --- class: inverse ### Standardized effect size in LMMs - The variance of expected mark for females is the standard error of the intercept squared: `$$0.0235^2 = \sigma^2_{\text{female}}$$` -- - The variance of expected mark for males is the sum of the standard error of the intercept squared and the standard error of the effect of gender squared, plus twice their covariance: `$$\sigma^2_{\text{female}} + 0.0210^2 + \underbrace{2\, r \, \sigma_{\text{female}}\times 0.0210)}_{\text{covariance} \\( r \text{ is the correlation}\\ \text{of fixed effects})}= \sigma^2_{\text{male}}$$` -- - see [variance of the sum of random variables](https://en.wikipedia.org/wiki/Propagation_of_uncertainty#Example_formulae): `$$\sigma^2_{A+B}=\sigma^2_{A} + \sigma^2_{B} + 2\,\underbrace{ r \, \sigma_{A} \,\sigma_{B}}_{\text{cov}(A,B)}$$` --- class: inverse ### Standardized effect size in LMMs - To calculate the pooled variance, we take into account that there are 530 females and 120 males in the dataset, `$$\sigma^2_{\text{pooled}} = \frac{(530-1)\sigma^2_{\text{female}} + (120-1)\sigma^2_{\text{female}}}{530 + 120 -2}$$` -- - Here is the estimate of effect size as estimated by the LMM model `$$\text{Cohen's }d = \frac{\beta_{\text{gender}}}{\sqrt{\sigma^2 + \sigma^2_{\text{pooled}}+ \tau_{\text{student}}+ \tau_{\text{module}} }} \approx -0.15$$`