class: title-slide, center, inverse # Numerical & mathematical skills for neuroscience # PS5210 ## Matteo Lisi ### Part 2: introduction to linear algebra --- class: inverse ## Vocabulary - vector - matrix - linear combination - linear (in)dependence - basis - span - transformation - eigenvalues & eigenvectors --- ### Vectors - A list of `\(n\)` numbers representing a point, or an "arrow", in `\(n\)`-dimensional space -- - The vector `\(\overrightarrow{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \in \mathbb{R}^2\)` represents a point/arrow in a 2-dimensional space <!-- .center[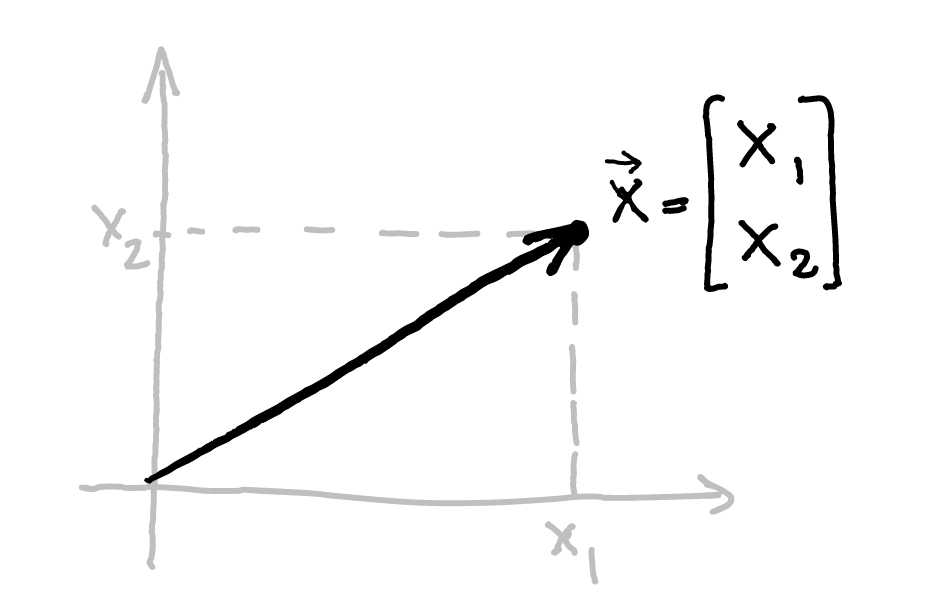] --> <img src="slides_numerical_skills_part2_files/figure-html/unnamed-chunk-1-1.svg" width="40%" style="display: block; margin: auto;" /> --- ### Vectors - A 3-dimensional vector .center[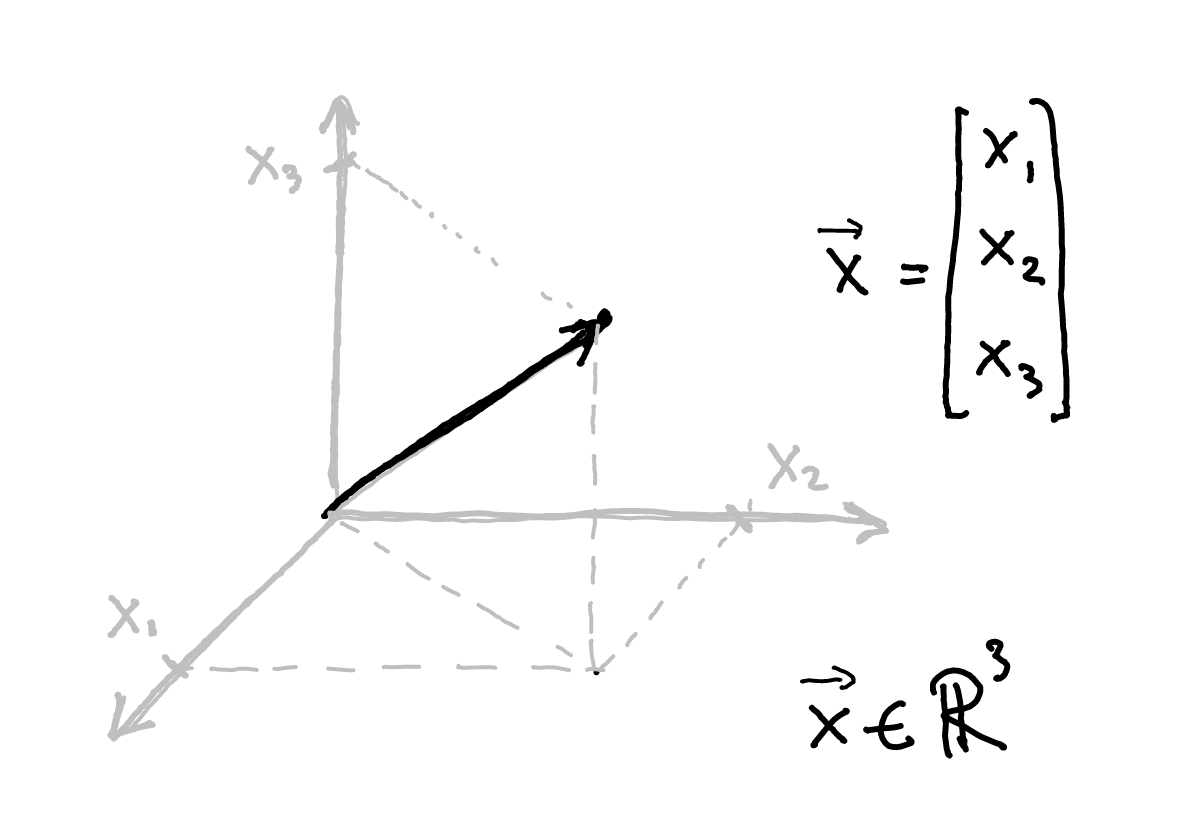] --- ### Sum of vectors .center[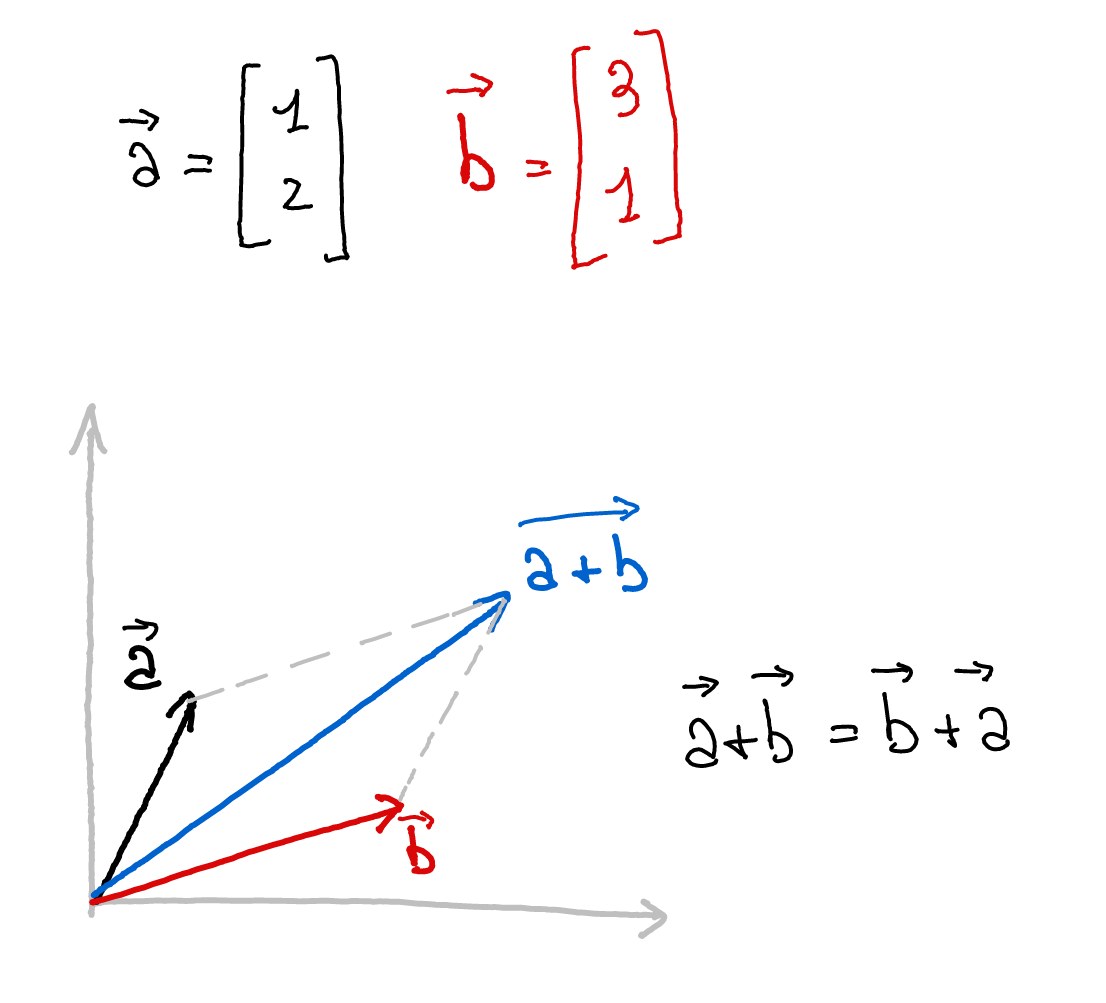] --- #### Multiplication of a vector with a single number (_scalar_) .center[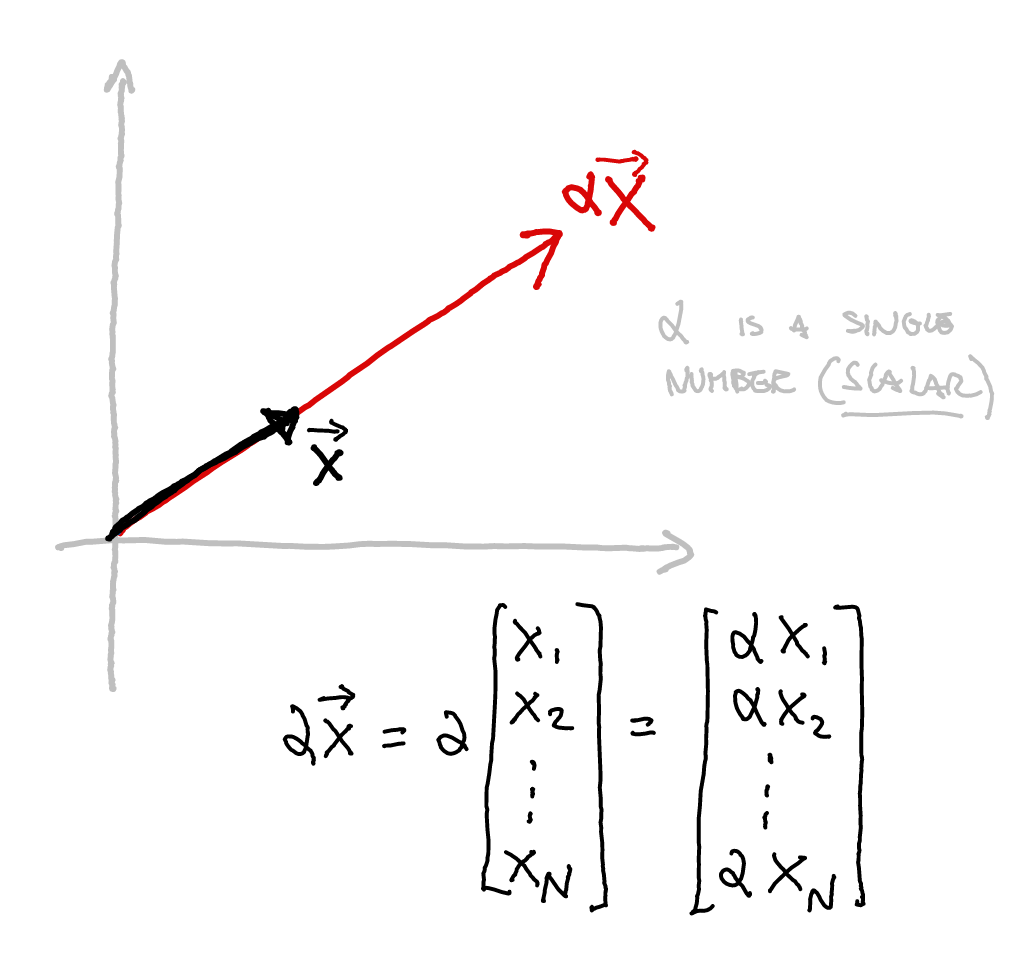] --- #### Elementwise vector multiplication (Hadamard product) <!-- .center[] --> `$$\vec{x} \circ \vec{y} = \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} \circ \begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix} = \begin{bmatrix} x_1y_1 \\ \vdots \\ x_ny_n \end{bmatrix}$$` -- In Matlab, you can achieve this with `x .* y` --- ### Linear combination of vectors <!-- .center[] --> `$$c\,\vec{\bf{v}} + d\, \vec{\bf{w}} = c \begin{bmatrix} 1 \\ 1 \end{bmatrix} + d \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} c + 2d \\ c + 3d \end{bmatrix}$$` -- .red[_How do you describe the set of **all** possible combinations of] `\(\overrightarrow{v}\)` .red[and] `\(\overrightarrow{w}\)`.red[?_] -- This is referred to as the **span** of the set of vectors `\(\left\{\overrightarrow{v}, \overrightarrow{w}\right\}\)`. In this case the combinations of `\(\overrightarrow{v}\)` and `\(\overrightarrow{w}\)` fill a whole two-dimensional plane. --- ### Matrix-vector multiplication Multiplying a matrix by a vector is like taking linear combinations of the matrix's columns <!-- .center[] --> `$$c\vec{v} + d\vec{w} = c \begin{bmatrix} 1 \\ 1 \end{bmatrix} + d \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} c + 2d \\ c + 3d \end{bmatrix}$$` -- <!-- .center[] --> `$$\mathbf{A}\vec{x} = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} c + 2d \\ c + 3d \end{bmatrix}$$` --- class: inverse ### Linear models -- The dependent variable `\(y\)` is modeled as a weighted combination of the predictor variables, plus an additive error `\(\epsilon\)` `$$y_i=\beta_0 + \beta_1x_{1i} + \ldots +\beta_nx_{ni} + \epsilon_i \\ \epsilon \sim \mathcal{N}\left( 0, \sigma^2 \right)$$` --- class: inverse count: false ### Linear models The dependent variable `\(y\)` is modeled as a weighted combination of the predictor variables, plus an additive error `\(\epsilon\)` `$$\textbf{Y} = \textbf{X}\beta + \epsilon \\ \epsilon \sim \mathcal{N}\left( 0, \sigma^2 \right)$$` -- Linear models: matrix notation `$$\bf{Y} = \bf{X}\beta + \epsilon$$` `$$\left( \begin{array}{c} y_1 \\ \vdots \\ y_m \end{array} \right) = \left( \begin{array}{cccc} 1 & x_{11} & \ldots & x_{1n}\\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_{m1} & \ldots & x_{mn} \end{array} \right) \left( \begin{array}{c} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_n \end{array} \right) + \left( \begin{array}{c} \epsilon_1 \\ \vdots \\ \epsilon_m \end{array} \right)$$` <!-- Matrix multiplication: --> <!-- $$ --> <!-- \left( \begin{array}{cc} a & b \\ c& d \end{array} \right) --> <!-- \left( \begin{array}{c} 1 \\ 2 \end{array} \right) = --> <!-- 1 \left( \begin{array}{c} a \\ c \end{array} \right) + --> <!-- 2 \left( \begin{array}{c} b \\ d \end{array} \right) = --> <!-- \left( \begin{array}{c} a + 2b \\ c+ 2d \end{array} \right) --> <!-- $$ --> --- ### Linear independence <!-- .center[] --> `$$\mathbf{A}\vec{x} = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} c + 2d \\ c + 3d \end{bmatrix}$$` `$$\mathbf{B}\vec{x} = \begin{bmatrix} 1 & 3 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} c + 3d \\ c + 3d \end{bmatrix}$$` .red[_How does the _span_ of the columns of A differ from the span of the columns of B?_] --- ### Vector dot product .center[] --- ### Vector dot product .center[] --- class:inverse ### Matrix multiplication * How do we multiply two matrices? -- * While there is only one correct way of doing it, we can about it in 2 slightly different ways: -- 1. as a series of dot products; -- 1. as a "combination of combinations" of columns. -- * This is the default operatin for the symbol `*` in Matlab. --- ### Matrix multiplication .center[] --- ### Matrix multiplication .center[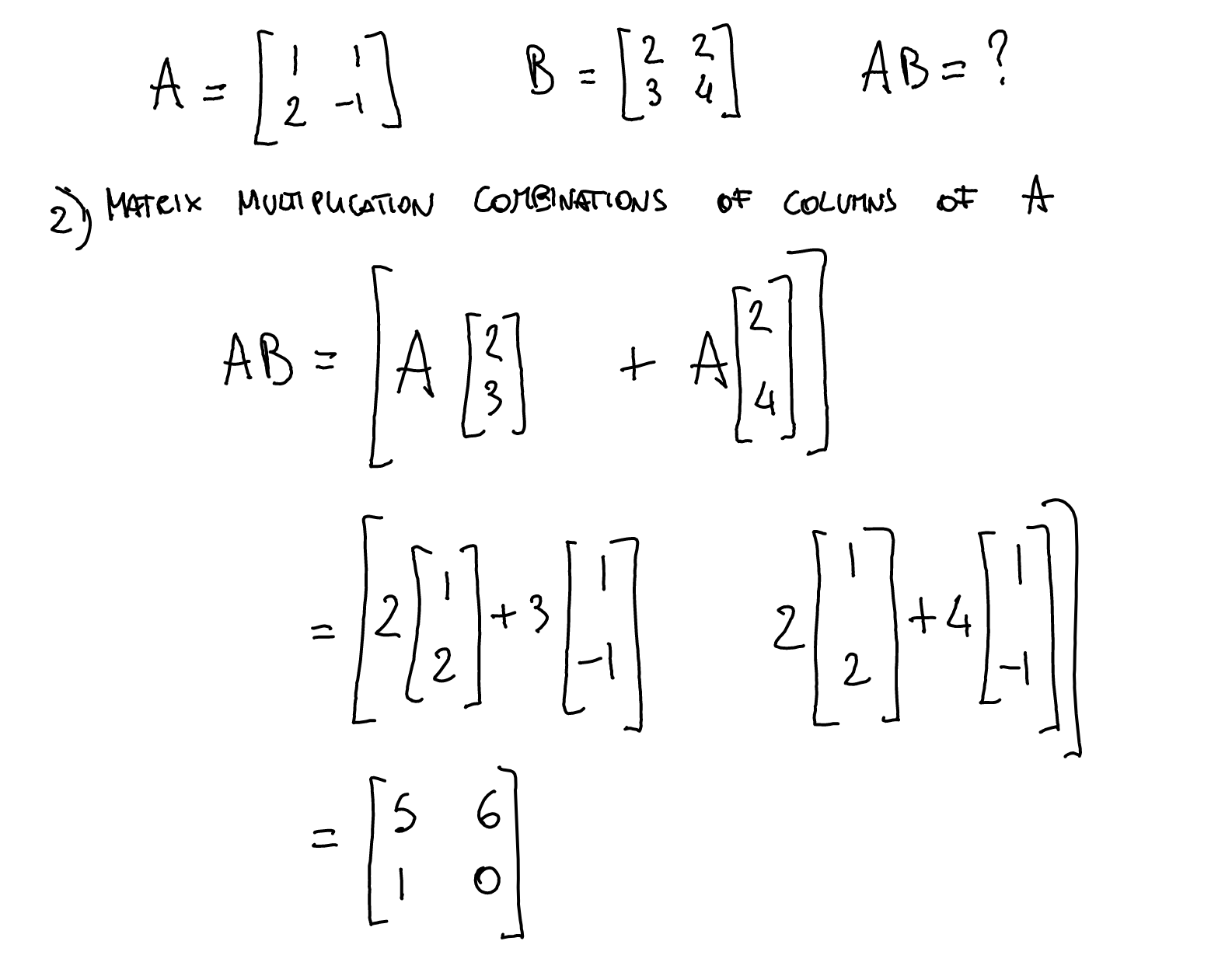] --- ### Matrix multiplication .center[] --- class:inverse ### What do we do with matrices? We can think of matrices as functions, which takes vectors as input and apply _transformations_ to them. `$$\overrightarrow{y} = f(\overrightarrow{x}) = A \overrightarrow{x}$$` --- ### Example: 'stretch' transformation .left-column[ `\(S = \begin{bmatrix} 1+\delta & 0 \\ 0 & 1\end{bmatrix}\)` `\(S \begin{bmatrix} x_1 & x_2 & \ldots \\ y_1 & y_2 & \ldots \end{bmatrix} = ?\)` ] .right-column[ <img src="slides_numerical_skills_part2_files/figure-html/unnamed-chunk-2-1.svg" width="80%" style="display: block; margin: auto;" /> ] --- ### Example: 'stretch' transformation .left-column[ `\(S = \begin{bmatrix} 1+\delta & 0 \\ 0 & 1\end{bmatrix}\)` <!-- .center[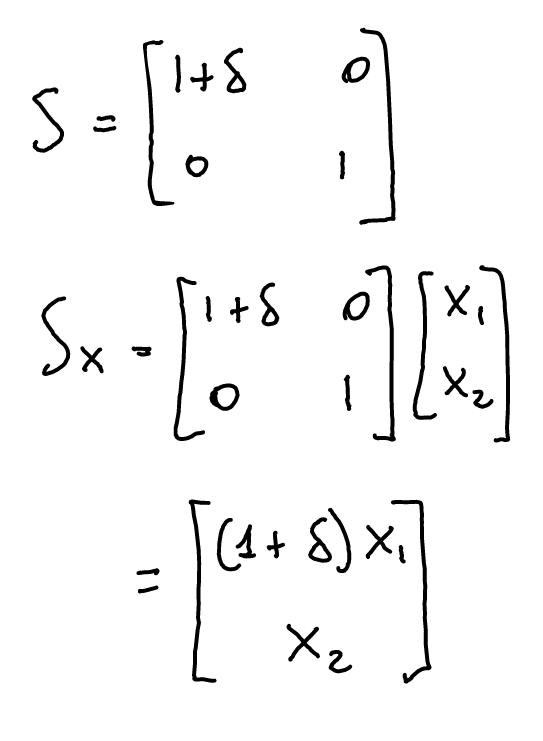] --> `\(\begin{align*} S &= \begin{bmatrix} 1 + \delta & 0 \\ 0 & 1 \end{bmatrix} \\ S\vec{x} &= \begin{bmatrix} 1 + \delta & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\ &= \begin{bmatrix} (1 + \delta)x_1 \\ x_2 \end{bmatrix} \end{align*}\)` ] .right-column[ <img src="slides_numerical_skills_part2_files/figure-html/unnamed-chunk-3-1.svg" width="80%" style="display: block; margin: auto;" /> ] --- class:inverse ### Special matrices Identity matrix: `\(I = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}\)` For any other matrix `\(A\)` we have that `\(AI = A = IA\)` --- class:inverse ### Special matrices Inverse matrix: `\(A^{-1}A=AA^{-1}=I\)` -- `\(S = \begin{bmatrix} 1+\delta & 0 \\ 0 & 1\end{bmatrix}\)` has inverse `\(S^{-1} = \begin{bmatrix} \frac{1}{1+\delta} & 0 \\ 0 & 1\end{bmatrix}\)` -- `\(SS^{-1} = \begin{bmatrix} 1+\delta & 0 \\ 0 & 1\end{bmatrix} \begin{bmatrix} \frac{1}{1+\delta} & 0 \\ 0 & 1\end{bmatrix} = \begin{bmatrix} \frac{1+\delta}{1+\delta} & 0 \\ 0 & 1\end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix} = I\)` --- ### Eigenvalues & Eigenvectors .center[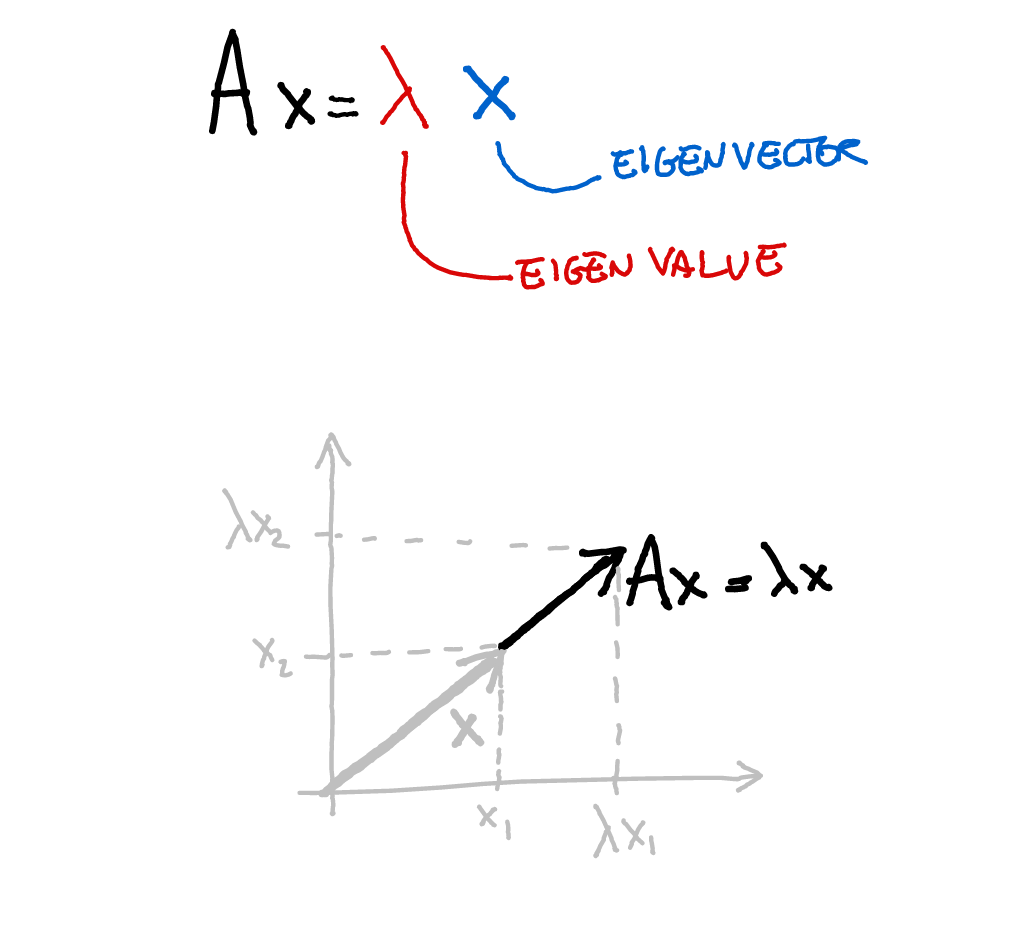] --- ### Eigenvalues & Eigenvectors .center[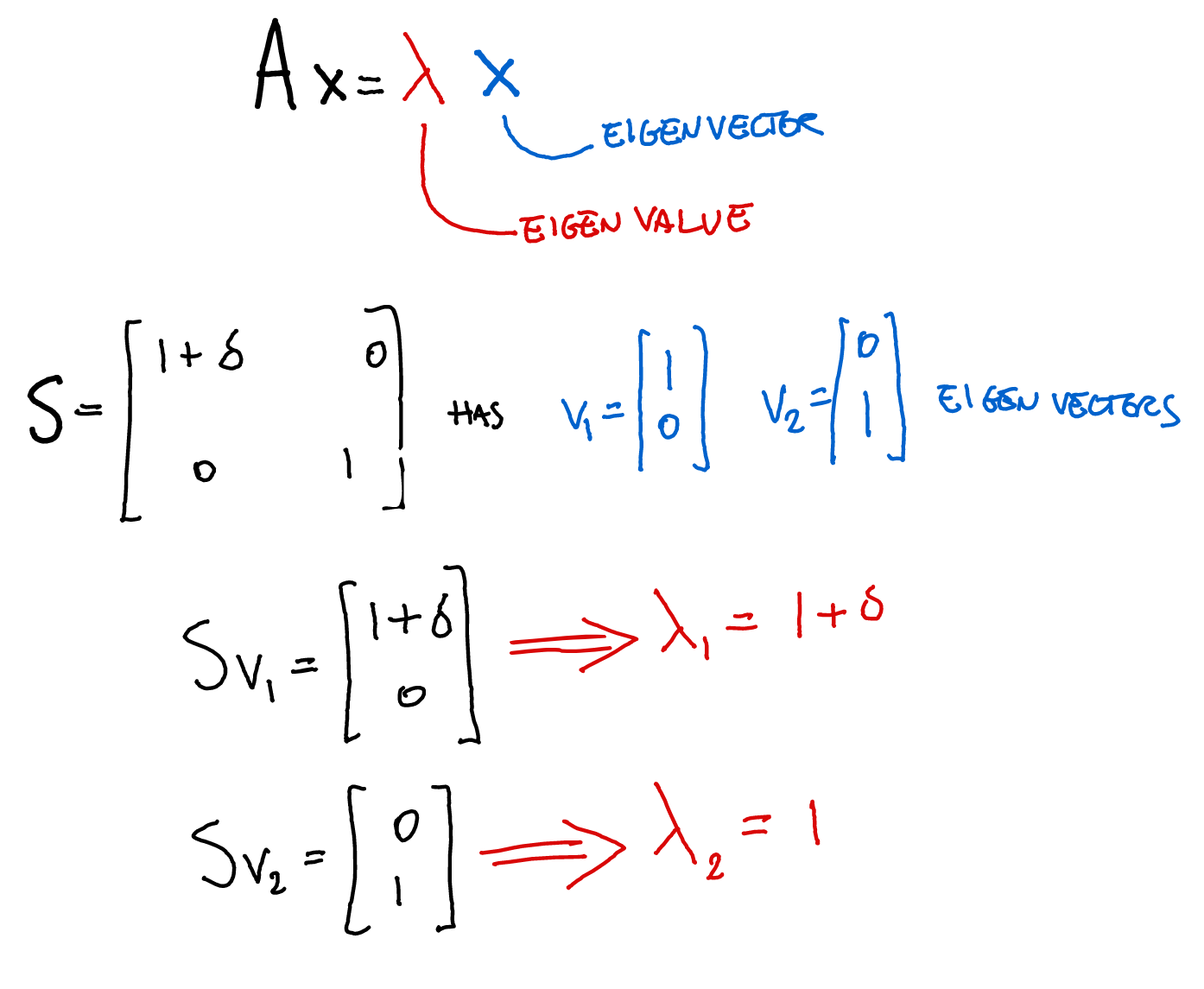] --- `\(Sv_1 = \begin{bmatrix} 1+\delta & 0 \\ 0 & 1\end{bmatrix} \begin{bmatrix} 1 \\ 0\end{bmatrix} = \begin{bmatrix} 1+\delta \\ 0\end{bmatrix} = (1+\delta ) \begin{bmatrix} 1\\ 0\end{bmatrix}= \lambda_1 v_1\)` `\(Sv_2 = \begin{bmatrix} 1+\delta & 0 \\ 0 & 1\end{bmatrix} \begin{bmatrix} 0 \\ 1\end{bmatrix} = \begin{bmatrix} 0 \\ 1\end{bmatrix} = 1 \begin{bmatrix} 0\\ 1\end{bmatrix}= \lambda_2 v_2\)` <img src="slides_numerical_skills_part2_files/figure-html/unnamed-chunk-4-1.svg" style="display: block; margin: auto;" /> --- class:inverse ### Principal component analysis (PCA) * A _dimensionality-reduction_ method -- * Given `\(n\)`-dimensional vectors (e.g. recording from `\(n\)` neurons) as data, we obtain a lower-dimensional representation, by projecting the data on a set of _principal components_, while preserving as much of the data's variation as possible. -- * Variance-covariance matrix: `\(\Sigma = \begin{bmatrix} \text{Var}(x_1) & \text{Cov}(x_1,x_2) & \cdots & \text{Cov}(x_1,x_n) \\ \text{Cov}(x_2,x_1) &\text{Var}(x_2) & \cdots & \text{Cov}(x_2,x_n)\\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}(x_n,x_1) & \text{Cov}(x_n,x_2) & \cdots & \text{Var}(x_n) \end{bmatrix}\)` -- * The eigenvectors of the variance-covariance are the principal components. -- * The eigenvector with the largest eigenvalue represents the direction of maximal variation in the data. --- ### Principal component analysis (PCA) `\(\Sigma = \begin{bmatrix} 1 & 0.99 \\ 0.99 & 1.5\end{bmatrix}\)` <img src="slides_numerical_skills_part2_files/figure-html/unnamed-chunk-5-1.svg" style="display: block; margin: auto;" /> --- ### Principal component analysis (PCA) Now showing the eigenvectors scaled by their respective eigenvalues. `$$\,$$` <img src="slides_numerical_skills_part2_files/figure-html/unnamed-chunk-6-1.svg" style="display: block; margin: auto;" /> --- class:inverse Matlab code for PCA on [Github](https://github.com/mattelisi/NeuroMethods) .center[]