The sleepstudy example

This dataset contains part of the data from a published study (Belenky et al. 2003) that examined the effect of sleep deprivation on reaction times. (This is a sensible topic: think for example to long-distance truck drivers.) The dataset contains the average reaction times for the 18 subjects of the sleep-deprived group, for the first 10 days of the study, up to the recovery period.

library(lme4)
Loading required package: Matrix
str(sleepstudy)
'data.frame':   180 obs. of  3 variables:
 $ Reaction: num  250 259 251 321 357 ...
 $ Days    : num  0 1 2 3 4 5 6 7 8 9 ...
 $ Subject : Factor w/ 18 levels "308","309","310",..: 1 1 1 1 1 1 1 1 1 1 ...

The model I want to fit to the data will contain both random intercepts and slopes; in addition the correlation between the random effects should also be estimated. Using lme4, this model could be estimated by using

lmer(Reaction ~ Days + (Days | Subject), sleepstudy)

The model could be formally notated as \[ y_{ij} = \beta_0 + u_{0j} + \left( \beta_1 + u_{1j} \right) \cdot {\rm{Days}} + e_i \] where \(\beta_0\) and \(\beta_1\) are the fixed effects parameters (intercept and slope), \(u_{0j}\) and \(u_{1j}\) are the subject specific random intercept and slope (the index \(j\) denotes the subject), and \(e \sim\cal N \left( 0,\sigma_e^2 \right)\) is the (normally distributed) residual error. The random effects \(u_0\) and \(u_1\) have a multivariate normal distribution, with mean 0 and covariance matrix \(\Omega\) \[ \left[ {\begin{array}{*{20}{c}} {{u_0}}\\ {{u_1}} \end{array}} \right] \sim\cal N \left( {\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right],\Omega = \left[ {\begin{array}{*{20}{c}} {\sigma _0^2}&{{\mathop{\rm cov}} \left( {{u_0},{u_1}} \right)}\\ {{\mathop{\rm cov}} \left( {{u_0},{u_1}} \right)}&{\sigma _1^2} \end{array}} \right]} \right) \]

In Stan, fitting this model requires preparing a separate text file (usually saved with the ‘.stan’ extension), containing several “blocks”. The 3 main types of blocks in Stan are:

• data all the dependent and independent variables needs to be declared in this blocks
• parameters here one should declare the free parameters of the model; what Stan do is essentially use a MCMC algorithm to draw samples from the posterior distribution of the parameters given the dataset
• model here one should define the likelihood function and, if used, the priors

Additionally, we will use two other types of blocks, transformed parameters and generated quantities. The first is necessary because we are estimating also the full correlation matrix of the random effects. We will parametrize the covariance matrix as the Cholesky factor of the correlation matrix (see my post on the Cholesky factorization), and in the transformed parameters block we will multiply the random effects with the Choleki factor, to transform them so that they have the intended correlation matrix. The generated quantities block can be used to compute any additional quantities we may want to compute once for each sample; I will use it to transform the Cholesky factor into the correlation matrix (this step is not essential but makes the examination of the model easier).

d_stan <- list(Subject = as.numeric(factor(sleepstudy$Subject, 
    labels = 1:length(unique(sleepstudy$Subject)))), Days = sleepstudy$Days, 
    RT = sleepstudy$Reaction/1000, N = nrow(sleepstudy), J = length(unique(sleepstudy$Subject)))

data {
  int<lower=1> N;            //number of observations
  real RT[N];                //reaction times

  int<lower=0,upper=9> Days[N];   //predictor (days of sleep deprivation)

  // grouping factor
  int<lower=1> J;                   //number of subjects
  int<lower=1,upper=J> Subject[N];  //subject id
}

parameters {
  vector[2] beta;                   // fixed-effects parameters
  real<lower=0> sigma_e;            // residual std
  vector<lower=0>[2] sigma_u;       // random effects standard deviations

  // declare L_u to be the Choleski factor of a 2x2 correlation matrix
  cholesky_factor_corr[2] L_u;

  matrix[2,J] z_u;                  // random effect matrix
}

transformed parameters {
  // this transform random effects so that they have the correlation
  // matrix specified by the correlation matrix above
  matrix[2,J] u;
  u = diag_pre_multiply(sigma_u, L_u) * z_u;

}

model {
  real mu; // conditional mean of the dependent variable

  //priors
  L_u ~ lkj_corr_cholesky(1.5); // LKJ prior for the correlation matrix
  to_vector(z_u) ~ normal(0,2);
  sigma_e ~ normal(0, 5);       // prior for residual standard deviation
  beta[1] ~ normal(0.3, 0.5);   // prior for fixed-effect intercept
  beta[2] ~ normal(0.2, 2);     // prior for fixed-effect slope

  //likelihood
  for (i in 1:N){
    mu = beta[1] + u[1,Subject[i]] + (beta[2] + u[2,Subject[i]])*Days[i];
    RT[i] ~ normal(mu, sigma_e);
  }
}

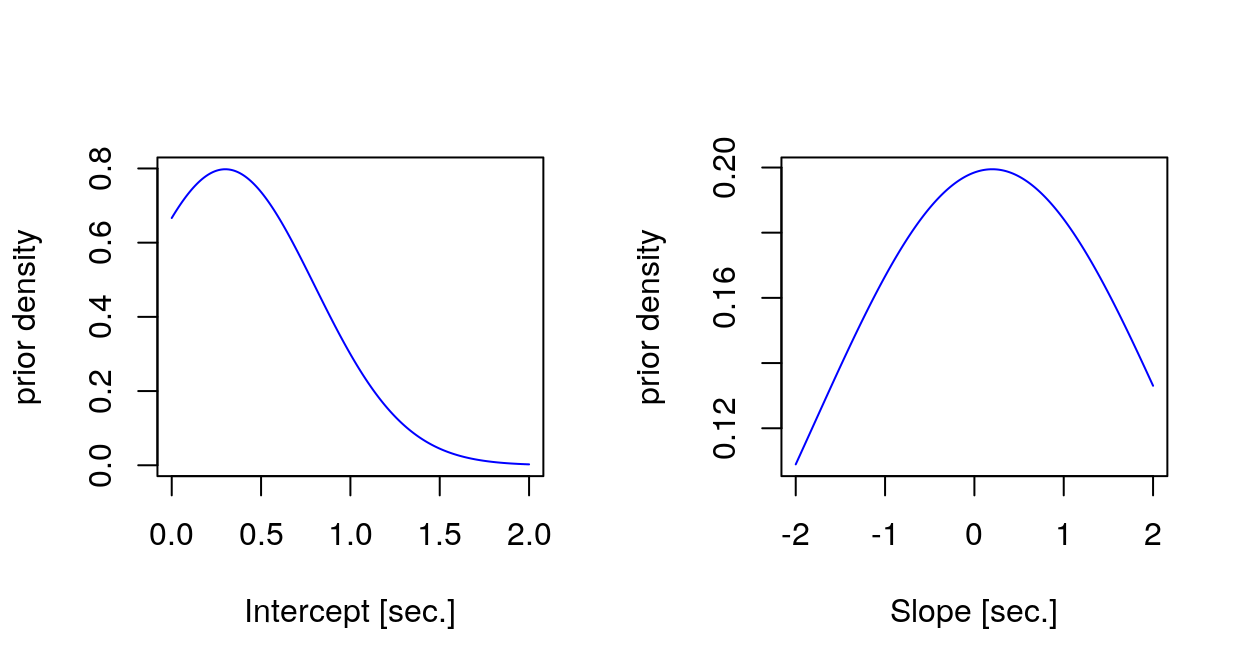
generated quantities {
  matrix[2, 2] Omega;
  Omega = L_u * L_u'; // so that it return the correlation matrix
}

Estimating the model

Having written all the above blocks in a separate text file (I called it “sleep_model.stan”), we can call Stan from R with following commands. I run 4 independent chains (each chain is a stochastic process which sequentially generate random values; they are called chain because each sample depends on the previous one), each for 2000 samples. The first 1000 samples are the warmup (or sometimes called burn-in), which are intended to allow the sampling process to settle into the posterior distribution; these samples will not be used for inference. Each chain is independent from the others, therefore having multiple chains is also useful to check the convergence (i.e. by looking if all chains converged to the same regions of the parameter space). Additionally, having multiple chain allows to compute a statistic which is also used to check convergence: this is called \(\hat R\) and it corresponds to the ratio of the between-chain variance and the within-chain variance. If the sampling has converged then \({\hat R} \approx 1 \pm 0.01\). When we call function stan, it will compile a C++ program which produces samples from the joint posterior of the parameter using a powerful variant of MCMC sampling, called Hamiltomian Monte Carlo (see here for an intuitive explanation of the sampling algorithm).

library(rstan)
options(mc.cores = parallel::detectCores())  # indicate stan to use multiple cores if available
sleep_model <- stan(file = "sleep_model.stan", data = d_stan, 
    iter = 2000, chains = 4)

One way to check the convergence of the model is to plot the chain of samples. They should look like a “fat, hairy caterpillar which does not bend” (Sorensen, Hohenstein, and Vasishth 2016), suggesting that the sampling was stable at the posterior.

traceplot(sleep_model, pars = c("beta"), inc_warmup = FALSE)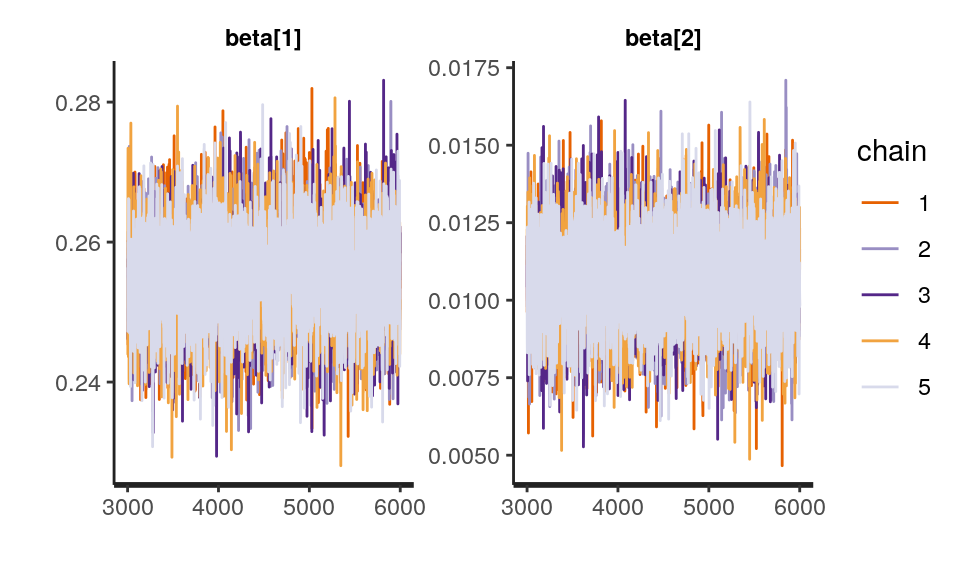

There is a print() method for visualising the estimates of the parameters. The values of the \({\hat R}\) (Rhat) statistics also confirm that the chains converged. The method automatically report credible intervals for the parameters (computed with the percentile method from the samples of the posterior distribution).

print(sleep_model, pars = c("beta"), probs = c(0.025, 0.975), 
    digits = 3)
Inference for Stan model: sleep_model_v1.
5 chains, each with iter=6000; warmup=3000; thin=1; 
post-warmup draws per chain=3000, total post-warmup draws=15000.

         mean se_mean    sd  2.5% 97.5% n_eff Rhat
beta[1] 0.255       0 0.006 0.243 0.268  6826    1
beta[2] 0.011       0 0.001 0.008 0.013  7830    1

Samples were drawn using NUTS(diag_e) at Sat Sep 22 17:15:42 2018.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

And we can visualze the posterior distribution as histograms (here for the fixed effects parameters and the standard deviations of the corresponding random effects).

plot(sleep_model, plotfun = "hist", pars = c("beta", "sigma_u"))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.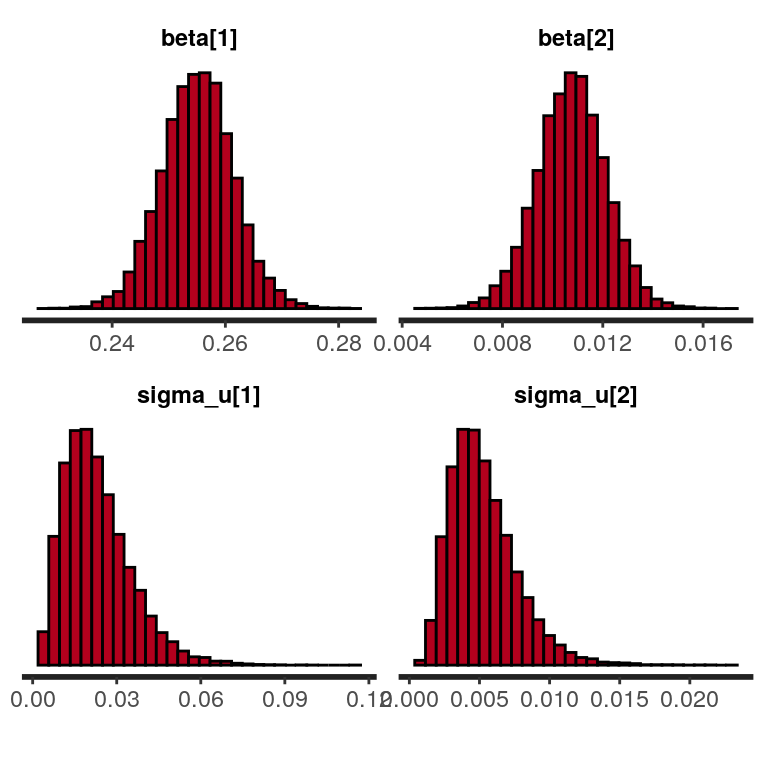

Finally, we can also examine the correlation matrix of random-effects.

print(sleep_model, pars = c("Omega"), digits = 3)
Inference for Stan model: sleep_model_v1.
5 chains, each with iter=6000; warmup=3000; thin=1; 
post-warmup draws per chain=3000, total post-warmup draws=15000.

            mean se_mean    sd   2.5%   25%   50%   75% 97.5% n_eff  Rhat
Omega[1,1] 1.000     NaN 0.000  1.000 1.000 1.000 1.000 1.000   NaN   NaN
Omega[1,2] 0.221   0.007 0.344 -0.546 0.011 0.251 0.467 0.807  2228 1.001
Omega[2,1] 0.221   0.007 0.344 -0.546 0.011 0.251 0.467 0.807  2228 1.001
Omega[2,2] 1.000   0.000 0.000  1.000 1.000 1.000 1.000 1.000   160 1.000

Samples were drawn using NUTS(diag_e) at Sat Sep 22 17:15:42 2018.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

The Rhat values for the first entry of the correlation matrix is NaN. This is expected for variables that remain constant during samples. We can check that this variable resulted in a series of identical values during sampling with the following command

all(unlist(extract(sleep_model, pars = "Omega[1,1]")) == 1)  # all values are =1 ?
[1] TRUE

That’s all! You can check by yourself that the values are the sufficiently similar to what we would obtain using lmer, and eventually experiment by yourself how the estimates changes when more informative priors are used. For more examples on how to fit linear mixed-effects models using Stan I recommend the article by Sorensen (Sorensen, Hohenstein, and Vasishth 2016), which also show how to implement crossed random effects of subjects and item (words), as it is conventional in linguistics.